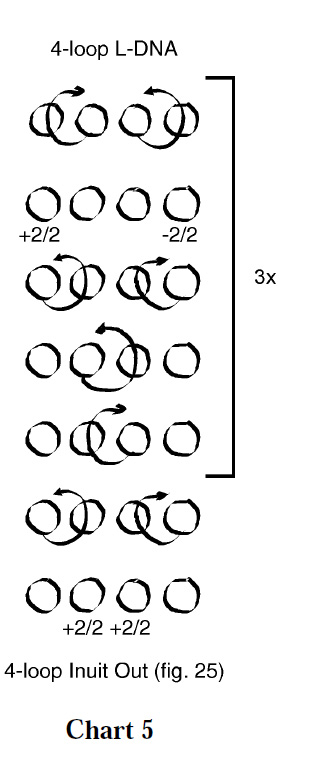
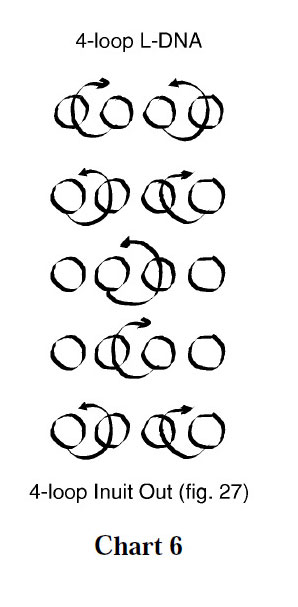When illustrated using circle notation, it’s easy to grasp the underlying symmetry of the prototypical 4-loop tennis net. In Line 2 of chart 5, the passage of the index loop up through the thumb loop is counterbalanced by a symmetrical passage of the middle finger loop up through the little finger loop. In Line 3, the +2/2 rotation of the thumb loop is counterbalanced by a -2/2 rotation of the little finger loop. The symmetry in the chart is reflected in the woven design.
Many beautiful variations of the prototypical 4-loop Tennis Net can be designed on paper, long before they are formed on the hands, by simply altering its circle notation chart. Below are a few examples.
Variation 1 (fig. 27, chart 6, page 254) is a greatly simplified version of the prototypical 4-loop tennis net.
When chart 6 is compared to chart 5, one immediately sees that all loop rotations have been omitted and the weaving sequence is done only once (use a loop made from a 2½-span string for this simple net).
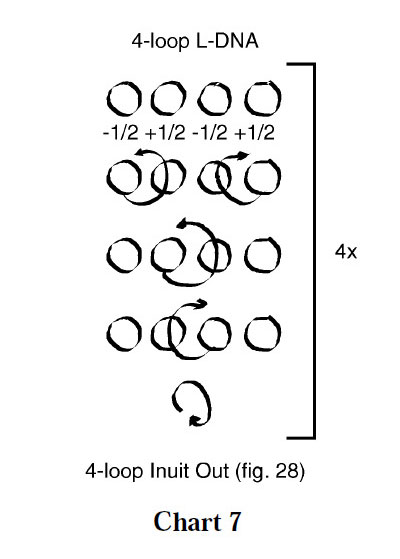
In Variation 2 below, chart 7, all loops are rotated a half turn at the beginning of each iteration and the entire figure is rolled at the end of each iteration.
Note that the number of iterations performed must be a multiple of two because of the half rotations introduced into the thumb and little finger loops at the beginning of each set. If an odd number of iterations is performed, the transverse frame lines of the final design will not be properly positioned.
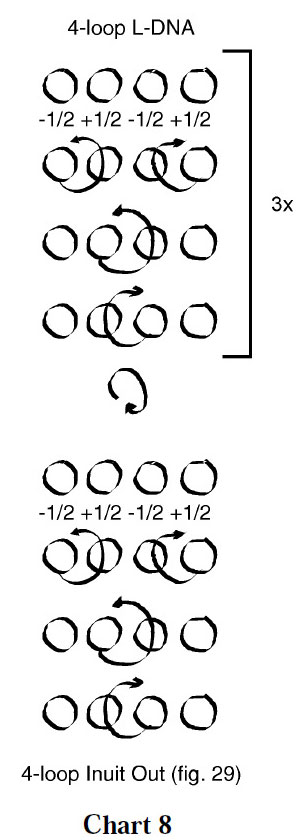
Variation 3, chart 8, below is the same as variation 2 except that the figure is not rolled until the beginning of the fourth iteration. Because of this the internal transverse strings loop around the frame lines once. This effect is particularly striking when the figure is woven with an octagonal two-color loop, as shown below.
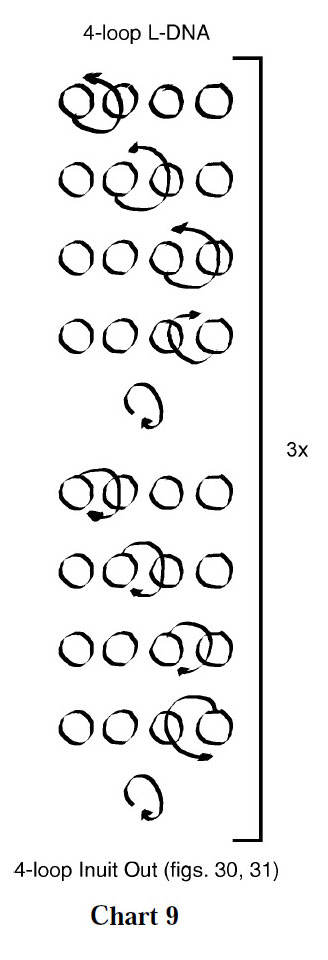
The algorithm for Variation 4 (figs. 30 and 31, chart 9) is remarkably simple:each loop is passed up through the adjacent loop, starting with the thumb loop. The figure is then rolled and the procedure repeated, but this time each loop is passed down through an adjacent loop. The creates small “towers” or “pagodas” within the mesh.
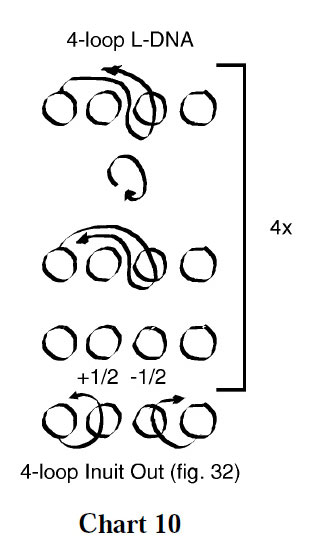
In Variation 5 (immediately below, fig. 32, chart 10) a single loop passage is repeated over andover. Between each loop passage the figure is either rolled or internal loops are rotated a half turn. The final design resembles a Ten Men variation called ‘Jaguar’ which i described in the ten men book part of this series.
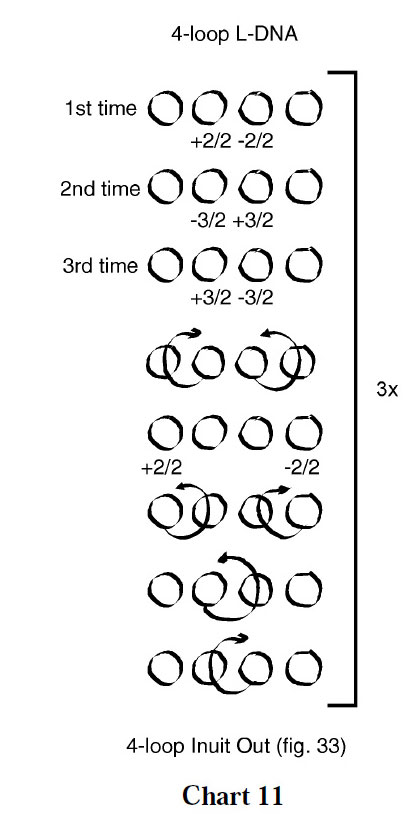
In Variation 6 (fig. 33, chart 11), loop rotations precede the prototypical 4-loop Tennis Net algorithm (the bracketed sequence in chart 5). However, the direction and degree of twisting varies with each iteration. At the beginning of the first iteration, the index loop is rotated +2/2 and the middle finger loop is rotated –2/2; at the beginning of the second iteration the index loop is rotated –3/2 (one and a half turns toward you) and the middle finger loop is rotated +3/2 (one and a half turns away from you); at the beginning of the third iteration the index loop is rotated +3/2 and the middle finger loop is rotated –3/2. The last iteration is followed immediately by 4-loop Inuit Out.
Don’t be afraid to design some variations of your own. The six examples given above merely illustrate how loop passages and loop rotations can be shuffled, regrouped, and iterated to create hundreds of interesting designs.
Very few moves are forbidden: a design of some sort will emerge as long as the near thumb and far little finger strings are transverse before applying the 4-loop Inuit Out ending. And don’t be discouraged by the fact that these figures fail to dissolve when the centers of the transverse strings are pulled in opposite directions. This minor flaw occurs because of the way the loops are “braided” during the loop passage maneuvers. The fastest way to undo a 4-loop Tennis Net is to lay the figure on your lap and patiently unbraid the loops by starting at the ends and working your way towards the center of the design.