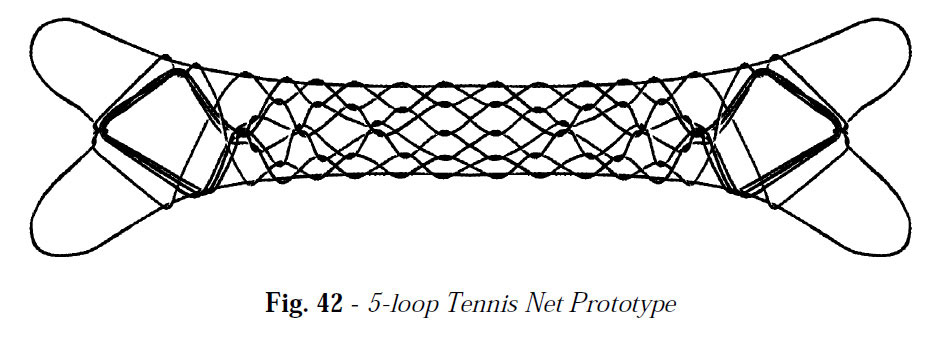
Weaving a 5-loop tennis net requires tremendous concentration since every finger is utilized in its formation. A loop made from a 4-span string is essential.
One would think that the presence of a fifth loop would exponentially increase the number of interesting patterns one can form. But because 5-loop looms have an odd number of loops, many of the symmetrical operations commonly employed in the weaving of 4-loop tennis nets do not have obvious counterparts in a 5-loop environment (for example, index loop up through middle finger loop followed by middle finger loop up through index loop). In my mind, string figures made from 2- and 4-loop looms constitute one family while figures made from 3- and 5-loop looms constitute another.
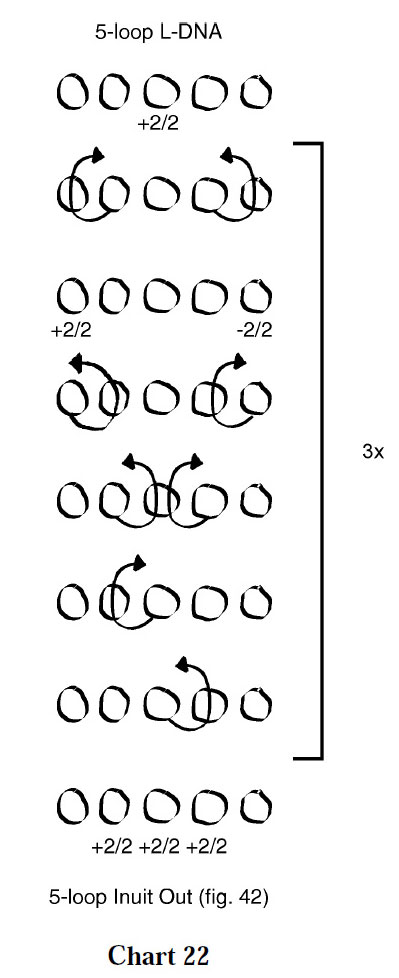
A prototypical 5-loop tennis net is not easy to define. One attempt is illustrated in chart 22 (figure below).
The first few loop passages of the 4-loop tennis net are easy to mimic in a 5-loop environment since only the outermost loops are involved. But subsequent passages, in which the inner loops are manipulated, are more difficult to copy. In chart 22, the index and ring finger loops are passed up through the middle finger loop followed by middle up through index and middle up through ring.
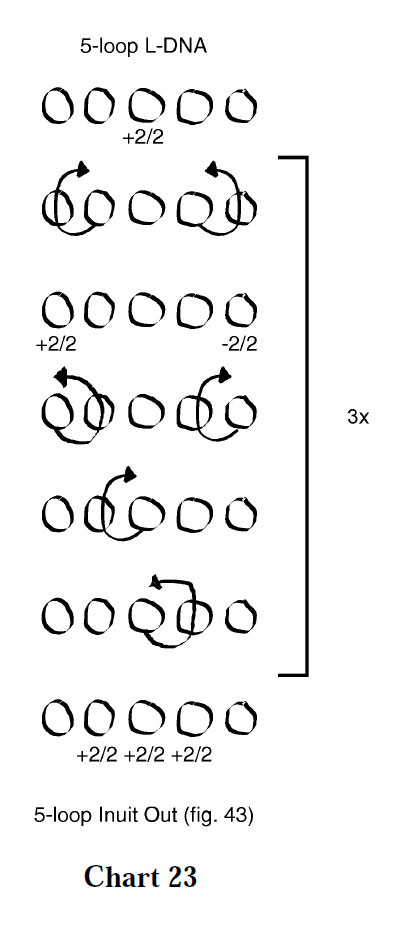
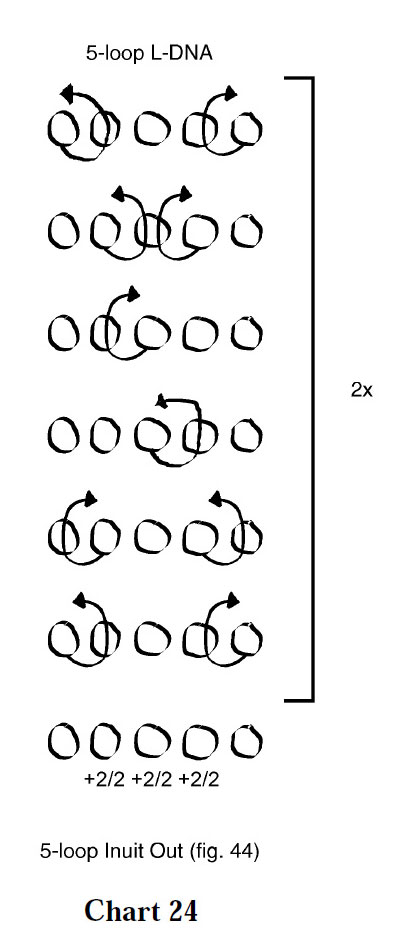
Other early attempts which i recently found in some of my older notebooks are shown in charts 23-26.
In Variation 1 (chart 23, figure below), doubled strings emanate from the central diamond and wind their way through the figure. Doubled strings also coil around the frame lines like snakes.
Variation 2 (chart 24, figure below) is similar but lacks doubled strings.
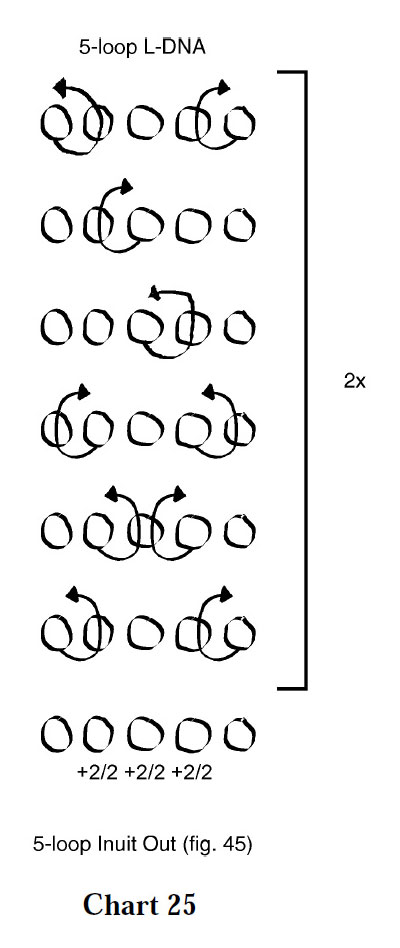
Variation 3 (chart 25, figure below) features a central rod-shaped knot surrounded by four large holes.
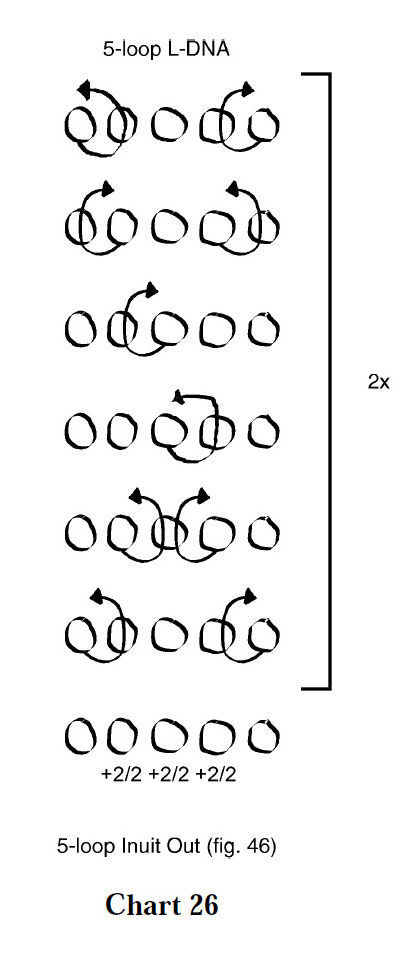
A pleasing octagon occupies the center of Variation 4 (chart 26, figure below).
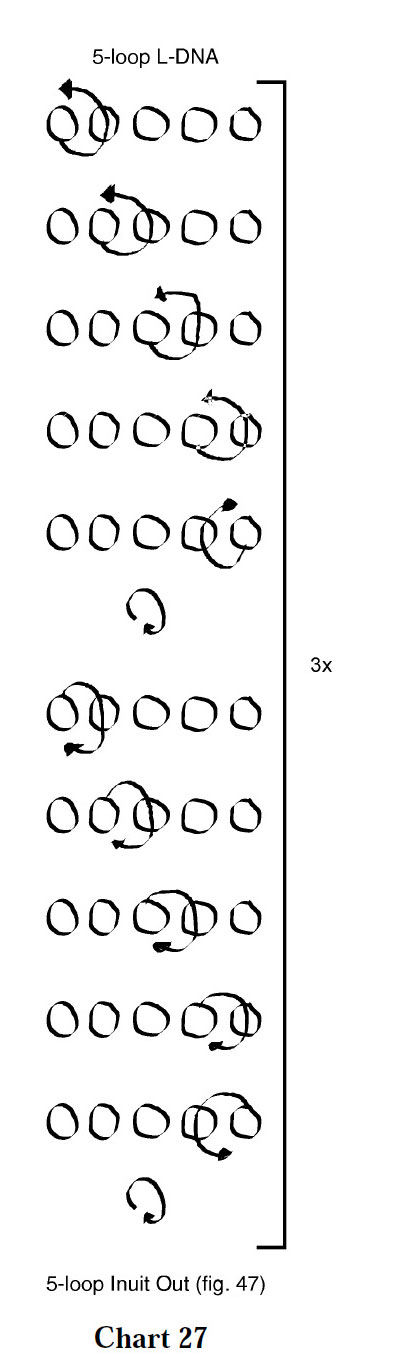
Also impressive is the figure below (variation 4, chart 27).
Like its 4-loop counterpart, this figure features “towers” embedded in the web. This effect is created by passing each loop up through its adjacent loop, rolling the figure, then passing each loop down through its adjacent loop and rolling again.
As in the 4-loop system, there are a multitude of finishing moves that one can apply after the iterative phase of any 5-loop tennis net. These include:
• (1) thumb loop up through index loop; little finger loop up through ring finger loop.
• (2) thumb loop up through index loop; little finger loop up through ring finger loop; index loop up through middle finger loop; ring finger loop up through middle finger loop.
• (3) (1) or (2) followed by +2/2 rotation of middle finger loop
• (4) (1) or (2) followed by +2/2 rotation of index, middle, and ring finger loops.
• (5) rotation of thumb loop +2/2 and little finger loop –2/2 followed by (1) or (2) or (3).
• (6) (2) followed by middle finger loop up through index loop; middle finger loop up through
ring finger loop.
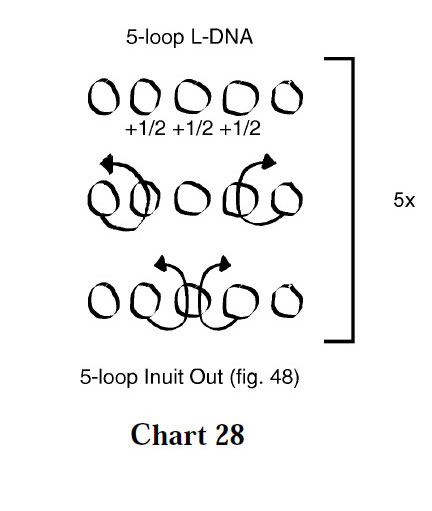
Inner loop rotations (rotations of the index, middle, or ring finger loops) add complexity to the final design. These can be confined to the initial loom alone, or repeated with each iteration of the main weaving sequence as illustrated by Variation 6 (figure below, chart 28)
The weaving sequence of Variation 6 is remarkably simple, yet a complex design results because of the repetitive loop rotations.
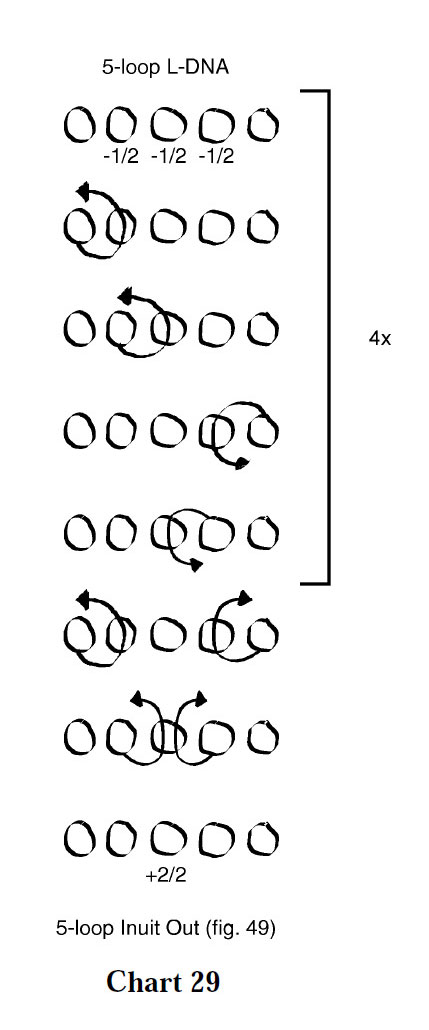
and Variation 7 (figure below, chart 29).
A new type of symmetry is apparent in the chart for Variation 7. The outermost loop passages are of opposite direction (thumb loop up through index loop, but little finger down through ring finger loop). The same is true of the innermost loop passages (index loop up through middle finger loop; ring finger loop down through middle finger loop).
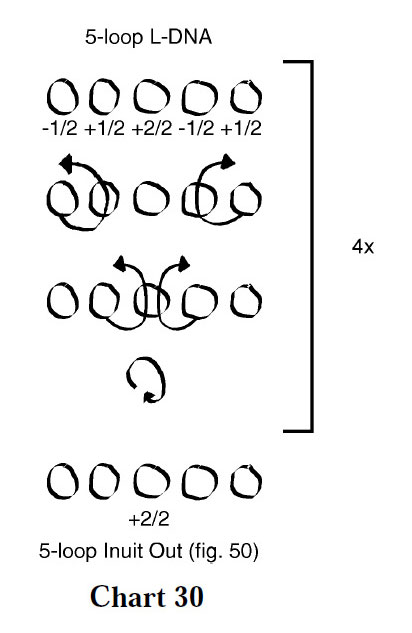
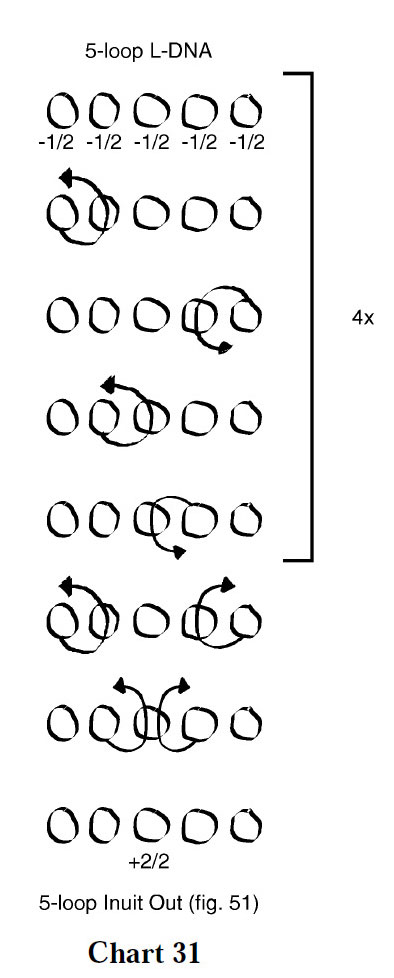
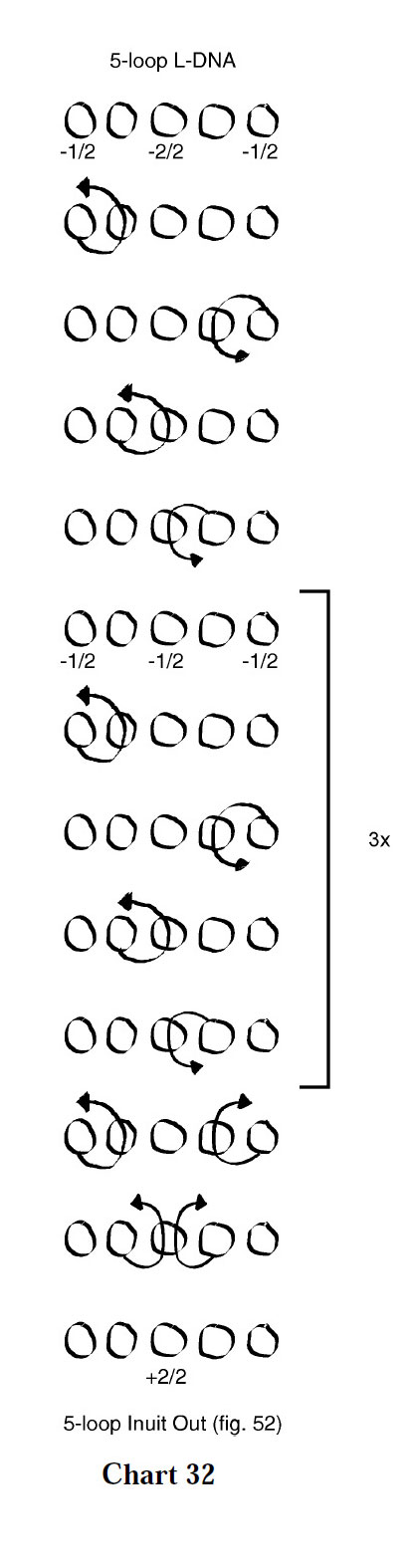
However, when half-rotations are introduced into the thumb and/or little finger loops, an even number of iterations must take place before finishing moves are applied so that the near thumb and far little finger strings, which are transverse in the initial loom, are once again transverse. Examples can be found in charts 30-32.
Note that in each example, half-rotations of the outermost loops are done a total of four times.
In Variation 8 (figure below, chart 30),
above the four outermost loops all receive half rotations whereas the innermost loop (the middle finger loop) receives a full rotation.
In Variation 9 (figure below, chart 31), all five loops receive a half rotation with each iteration.
In Variation 10 (figure below, chart 32), the first iteration differs from the subsequent three iterations, yet a total of four are performed in order to restore the positions of the frame strings.