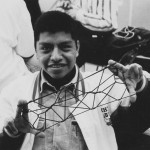
The focus of my approach to math using string figures is to teach a student’s hands to form geometric patterns, pretty pictures, on their own hands. This is a proving to self of success. It is impossible to get less than a 100 on making a successful string figure.

Your hands can probably now be said to be “dumb” in terms of their “knowing” string figures; that they cannot “think” in any abstract way, in any “complicated” way. (That is, unless you are a musician who has “learned” music patterns of your hands, or on your instrument.) With string figures your hands will be clumsy in their initial learning, but then become more and more nimble, and quicker in their “thinking” through.

There aren’t many basic figures which must be learned in order to become quite proficient at making figures of astounding beauty. There is a simple algebra which can lead into detailed inventiveness of wild and exciting patterns emerging on the students hands.

There will be videos, and detailed help to enable a student to learn to form these basic figures by rote, and then, by practice, by “making”, by “forming”, by “concatenating” precise strings of exact operations; to make unique string figures.

One should practice each of these basic patterns (one at a time in the beginning) until they become an instinctive, automatic, “natural” feeling as the hands dance in forming the patterns.

String figures are a visually pleasing way, and a wonderfully “tactile” way, of learning to appreciate complex consequential phenomena. You will be amazed at how quickly students will push for their own figure when they pick up speed and success in their searching difference. They will be led to become quicker and quicker at seeing detailed visual information almost instantaneously, and will gain a concomitant ability to see immediately the crucial elements to appreciate in any such complex situation.

Thus you can “learn to learn” mathematics, and/or any other intellectual pursuit, by what a successful experience with string figures teaches. It teaches persistence, and concentration, and assuredness as to eventual success. This latter is the most crucial lesson of all, except maybe for patience. All my students value the lesson they absorb of how to be more patient.

The public schools in the United States today are too often in a state of disarray. You as parents must begin to think of how you can prepare your children to succeed at whatever the future may hold for them. You must take full advantage of what the schools offer, and make sure they get a superior education. And to do this your children must become self motivated learning machines.

I have been involved with teaching string figures to children and teenagers for more than thirty years and have come to some hard and fast conclusions about how this is possible even given the current state of public education.

It is crucial that this training start early. The perfect time is the beginning of the first grade when each class should learn string figures together to set the tone for all future “school” learning.

I was first enamored of string figures when my mother noticed instructions of how to make some simple figures printed on the side of a box of starch. I wanted to learn more but my grandmother said, “they used to do that, but nobody remembers how today.” So that was that.

But a funny thing happened when I was 42 and teaching math in a public high school. I was asked by a student’s mother to teach a math/science hour on Saturdays in a program for gifted students. I needed the money and found the students were 10-11 years old and fidgety. So I resolved to find things for them to do rather than just fidget.

The second Saturday I rigged up an experiment to derive the notes of the scale using a knife edge to touch a string taut enough to give a musical tone at simple fractions of its length, 1/2, 1/3, 1/5, etc. The overtones produced cascade up in the normal western scale.

On the third Saturday I was prepared with teaching a string figure called ten men. I had found the figure in a book of string figures written by Caroline Furness Jayne in 1906 mostly about her collecting string figures among the various peoples brought to Saint Louis in 1904 for the world’s fair. It was a simple web and I figured out how to alter steps in its preparation to easily make thousands of new figures. So I had my lessons for the balance of the term. We investigated the possibility matrices of new figures and carefully recorded our findings.

I took this idea and introduced it into my teaching in La Guardia High School.. I was especially interested in helping the students who had had a disastrous experience in their math classes, and there were many of them in the school. Math is often viewed by students as immensely difficult and they often do worse in this class than their other classes (and often even fail).

I taught a full semester class in string figures for over twenty years and never had a student who did not blossom as a learner and succeed far beyond what they thought they were capable of. In the required five page paper at the end of the class each and every student reported a gain in confidence in their own ability to learn complex, hard material; and that they valued the patience they had also learned. This was most often explained as having to disentangle the string before making another figure and eventually understanding that a patient approach worked best for most tedious tasks.

They also all talked of how “playing” with the string helped them work through anxiety and anger. If they were upset they could take their string to a quiet place and make random figures for fifteen or twenty minutes and they were “cooled out”.

And I noticed an incredible level of bonding among the classmates who were intimately involved in helping each other with their string figures (and teaching each other the things they had individually discovered and invented).

I replicated these findings when I taught science in a program entitled “Prep For Prep”, a special program for minority students in the sixth grade throughout New York City. These students were put through a rigorous summer program followed by a Saturday schedule throughout the regular school year and a follow up summer. Then they were placed in prestigious private schools throughout the city (and thereby thoroughly integrating them). They were also followed throughout their college careers and helped in their finding a place in the adult world.

Needless to say this was very satisfying for me as I, again, concentrated on the lower performing entering students, and found I could help them tremendously in their confidence and ability to learn what they were asked to learn.

I also worked at a summer program for American Indian youth sponsored by the National Science Foundation and found they were especially helped by their learning of string figures.

I would go further when it comes time for a child to learn some complex “language” of thought. The most important and the first to be learned is one’s mother-tongue. (The reason for this nomenclature is that the language learned from one’s mother in England was different from the intellectual language of Latin!) This feat of learning is “unconscious” in the sense that there is no programmatic activity which is used to master it. It is organic and naturally inevitable.

The same cannot be said of the adjunct activities that go along with the intellectual flowering of the language ability, namely reading, writing, spelling, learning foreign languages. etc. These are generally studied programmatically, and often memorized.

Mathematics is another “language”, but not one learned in an “unconscious” natural way. It is approached as a “memorizable” discipline. Addition, subtraction, multiplication, and division can be (and should be) memorized as “tables” of combinatory results until the “answers” are ready to tongue or to hand when called forth. The idea is to practice until the answers come naturally without thought.

A “good” student can thus be said to be one who is adept at putting into an indelible memory bank the basic tables of information necessary to make a useful language of ideation out of math, science, poetry, history, etc. That is to say that they will sweat their way to the place of conversational ability in several complex matrices of descriptive thought.

Most students in the public school system rarely achieve this ability and consequently never learn how to learn enough to become adept at any intellectual discipline. This is the underlying problem of the school system.

What I feel is needed to combat this situation is not more of the same, but a radical difference in approaching the first “school learning” experiences. And if this experience can be made to be explosively successful then it will naturally become a part of the way every student will approach their future learning tasks.

Learning string figures as a set of mathematical systems of exploration and conjecture has all of the prerequisites of such a successful experience:

• it is fun.

• it is 100% successful.

• it is overwhelming in its insuring a success beyond one’s fondest dreams of success.

• it brings with it an appreciation of the strengths of patience.

• it demonstrates the especial power of dwelling on the mass of initial information needed to be “memorized” until it becomes one with the thinker/user of the language, until fluency is attained.

And there is another (even more crucial) concomitant to the experience of learning string figures as a mathematical language. It adds a language ability at an early enough age to make the later learning of disparate languages much easier. The example of the bilingual individual being compared to the polyglot illuminates this point. If an individual learns a second language and that is all, that person is hardly better prepared as an adult to learn a new language as an individual who is conversant only in his or her mother-tongue. However, someone who has learned three or four different languages as a young enough child becomes a polyglot and is empowered to learn with comparative ease new languages as an adult even if these languages are very different from the original languages learned! There seems to be a threshold of language-framework which is reached for other “details” to be inculcated with a fairly easy facility.

And there is usually the expectation on the part of the learners as to their eventual success which adds to the appropriate concentration necessary for the successful learning to take place.

Another way of encapsulating the power of this learning experience is to experience how it teaches you to practice until you have made real the following:

• how you can do it

• what you can do with it

• how it maps other endeavors

• and then, how easy it makes learning other things

And the intense interest level of all the children I have introduced to string figures insures a successful learning. This is a unique opportunity to shape a young person’s feelings about their intellectual abilities and about their capacity to learn. This should not be underestimated.